Pre Algebra och skolbesök

2011-09-12 Av Simon Rybrand 0 kommentarer

Vad kommer egentligen innan Algebra och förståelse av ekvationer, funktioner och Algebraiska uttryck? Kanske borde vi göra som jänkarna och införa mer pre algebra i våra skolor?

MatematikVideo på besök på Lövgärdesskolan

Idag var jag på besök på en skola i Göteborg för att prata matematik med en lärare på högstadiet. Vi diskuterade bland annat vilka behov det finns för elever i de åldrarna och vilka möjliga metoder det finns för att göra så bra undervisning som möjligt. Jag jobbar själv deltid som gymnasielärare i matematik så det var väldigt intressant att prata om matematik med en duktig lärare som jobbar på högstadiet. Dels för att lära sig mer själv men också för att förstå hur vi på MatematikVideo.se kan utveckla våra kurser i framtiden. Vi pratade bland annat om det som man i USA brukar kallas för pre algebra vilket vi båda tyckte var något som var viktigt att lyfta fram i den svenska matematikundervisningen.

Pre Algebra för att förstå Algebra

Pre Algebra kan sägas vara något vi kan jobba med innan vi sätter igång med ekvationer, ekvationssystem eller att beräkna funktioners värden. Man kan säga att det är en slags inkörsport för att mjuka upp och vänja våra hjärnor vid att jobba med bokstäver i matematiken. Det handlar framförallt att jobba algebraiskt med bilder, övningar och ord innan vi sätter igång med x:en och y:na. Att först få en känsla för hur man tänker i Algebran och att det framförallt inte är så stor skillnad på att räkna med bokstäver (dvs Algebra) och att räkna med tal (Aritmetik). Här på MatematikVideo.se kommer jag att ta med mig detta i mina planer framåt i grundkurser och pedagogiska upplägg.

Ett litet exempel på Pre Algebra

För att visa ett exempel på pre algebra som passar in på gymnasieundervisningen i matematik kan vi skapa en geometrisk bild för att förstå den distributiva lagen, dvs att

$ a \cdot (b + c) = ab + ac $

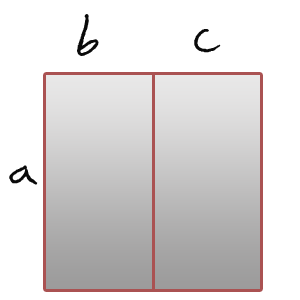
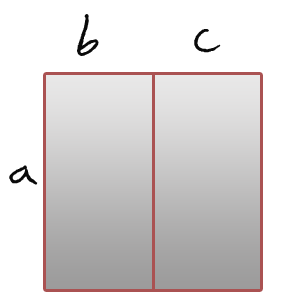
Två olika sätt att beräkna arean?

Istället för att direkt försöka förstå själva formeln kan vi fundera på hur vi räknar ut arean för kvadraten i figuren. Då kanske vi inser att det finns två olika sätt att beräkna arean. Dels kan den beräknas genom att ta a•(b + c) alltså höjden gånger bredden. Eller så kan vi beräkna varje rektangel för sig och få arean genom att beräkna a•b + a•c. Dvs a•(b + c) = a•b + a•c som ju är den distributiva lagen!

Alltså visar de två olika sätten att beräkna arean i figuren att vänsterledet = högerledet i formeln här ovan.

Det här är alltså ett sätt att mjuka upp förståelsen av vår formeln bildligt innan vi lär oss den som formeln. Kanske kan det vara något för dig?