
Exempel i videon
- Mattias är ute och kör på sin motorcykel. Vid ett tillfälle, när Mattias är $2,5$ km hemifrån,så kör han först i $15$ m/s i $20$ sekunder, varpå han sedan accelererar till hastigheten $35$ m/s under loppet av $10$ sekunder.
- Ett föremål släpps från en höjd och faller sedan fritt, tills dess att det slår i marken $3$ sekunder senare. Skissa föremålets kruva i en VT-graf.
- Världens bästa sprinter kan springa sträckan $400$ meter på lite drygt $44$ sekunder. Skissa en möjlig kurva i en VT-graf för ett sådant lopp.
VT-Grafen som verktyg
Tidigare har vi pratat om hur vi kan använda ST-grafen för att beskriva hur ett avstånd förändras med tiden.
På samma sätt så kan vi också använda en graf för att beskriva hur en hastighet förändras med tiden. En graf som uppfyller detta ändamålet är den s.k. VT-grafen.
I en VT-graf så motsvarar den lodräta axeln hastigheten för föremålet, medan den vågräta axeln fortfarande representerar tiden. På så sätt kan vi markera i grafen vilken hastighet ett föremål har vi en given tidpunkt.
Hur tolkar vi VT-grafen?
När det kommer till att tolka information ur en VT-graf så finns det vissa bra regler som man behöver komma ihåg.
- Höjden där kruvan bryter den lodräta axeln motsvarar hastigheten vid tiden $0$ sekunder. (Dvs starthastigheten.)
- En rak linje som inte lutar i en VT-graf motsvarar ett föremål som färdas med konstant hastighet.
- En rak linje som lutar motsvarar föremål med en konstant acceleration (som t.ex. föremål i fritt fall).
- Slutligen så kan startavståndet inte avläsas ur en VT-graf.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (3)
-
1. Premium
I en VT-graf så är enheten längs med den lodräta axeln:
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
2. Premium
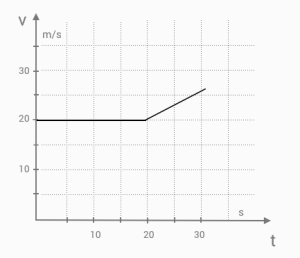
VT-grafen beskriver ovanför ett föremål som:
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
3. Premium
Vilket av följande alternativ kan man inte läsa av ur en VT-graf?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...

Endast Premium-användare kan kommentera.