
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 3b
/ Sammanfattning Ma3
Sammanfattning Matematik 3b
Innehåll
- Funktioner
- Polynom
- Algebra
- Rationellt uttryck
- Förenkla rationella uttryck
- Kvadreringsreglerna
- Konjugatregeln
- Potensregler
- Kvadratrötter
- Polynomfunktioner
- Polynomfunktionens graf
- Tips och vanliga fel vid ekvationslösning
- Fem sätt att lösa ekvationer på
- Ändringskvot/differenskvot, tangent och sekant
- Gränsvärde
- Derivatans definition
- Deriveringsregler
- Derivatan och tangentens lutning
- Växande och avtagande
- Bestäm extrempunktens karaktär
- Teckentabell
- Primitiva funktioner och integraler
- Integraler
- Geometriska talföljder
- Linjär optimering
- Repetitionsmaterial
- Kommentarer
![]() I sammanfattning Matematik 3b samlar vi formler och begrepp som du behöver kunna i kursen Matematik 3b. Du hittar lätt vad du söker i innehållsförteckningen här till höger.
I sammanfattning Matematik 3b samlar vi formler och begrepp som du behöver kunna i kursen Matematik 3b. Du hittar lätt vad du söker i innehållsförteckningen här till höger.
Vår fullständiga kurs hittar du här:
Sammanfattning Matematik 3b ger dig en överblick över kursen. Den hjälper vid repetition inför prov eller inför att du ska läsa Matematik 4.
Genom att klicka på länkarna i texten kommer du till lektioner med övningsuppgifter och videogenomgångar på de olika begreppen. På så sätt kan du fördjupa dig mer kring det som här, i all enkelhet, kort presenteras. Följ länken för att se hur skolverket beskriver kursens centrala innehåll.
En annan bra repetition av kursen är att göra nationella prov som gjort tidigare år. Vi har samlat dem på ett ställe.
Funktioner
En funktion är en regel som till varje tillåtet $x$x-värde ger exakt ett $y$y -värde. Du kontrollerar om en graf är en funktionen med hjälp av vertikaltestet.
Definitionsmängden är de tillåtna $x$x-värdena
Värdemängden är de erhållna $y$y-värdena
Funktioner delas in i kontinuerliga eller diskontinuerliga funktioner.
En funktion $f$ƒ är kontinuerlig då den är kontinuerlig i varje punkt i sin definitionsmängd.
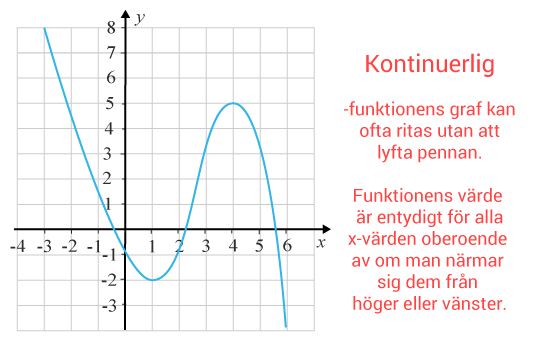
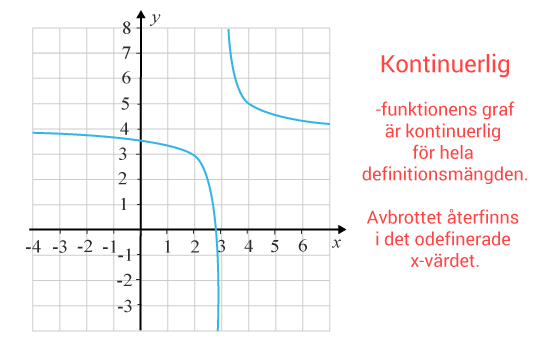
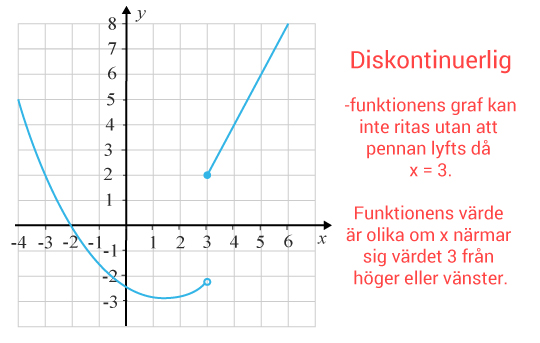
Om en funktion inte är kontinuerlig för alla punkter tillhörande definitionsmängden, är den diskontinuerlig. Det visar sig genom att grafer som tillhör en diskontinuerlig funktion innehåller ett eller flera ”glapp” även för $x$x-värden som tillhör definitionsmängden.
Polynom
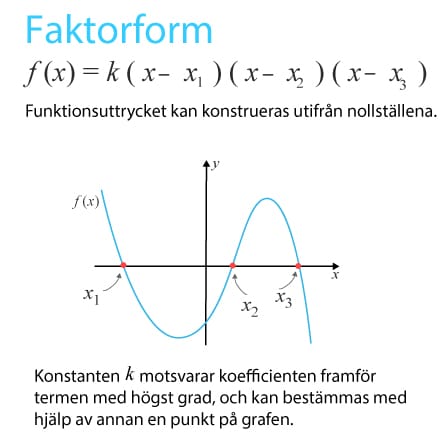
Polynom är en summa av termer där variabeln är i basen och alla exponenter tillhör de naturliga talen. Alla polynom kan skrivas i faktorform.
Algebra
En stor del av Matematik 3b handlar om att behärska algebra och alla dess olika räkneregler. Här sammanfattar vi de viktigaste du behöver kunna för att klara kursen.
Rationellt uttryck
Rationella uttryck definieras som en kvot av två polynom.
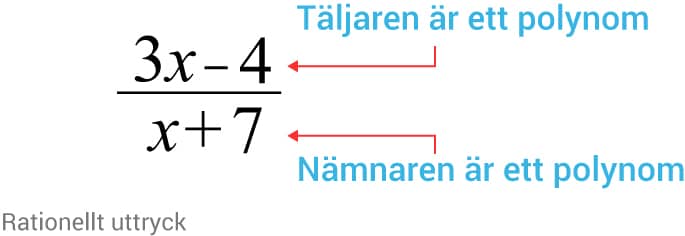
Mer matematiskt definierar vi ett rationellt uttryck $r\left(x\right)$r(x) som kvoten av två polynom $p(x)$p(x) och $q(x)$q(x).
$r\left(x\right)=$r(x)= $\frac{p\left(x\right)}{q\left(x\right)}$p(x)q(x) där $q(x)\ne0$q(x)≠0
Förenkla rationella uttryck
Genom att behärska kvadreringsreglerna och konjugatregeln kan du skriva om uttryck till faktorer, som du förhoppningsvis kan förkorta och på så vis förenkla tillsynes komplicerade rationella uttryck.
Kvadreringsreglerna
$(a+b)^2=a^2+2ab+b^2$(a+b)2=a2+2ab+b2
$(a-b)^2=a^2-2ab+b^2$(a−b)2=a2−2ab+b2
Konjugatregeln
$(a+b)(a-b)=a^2-b^2$(a+b)(a−b)=a2−b2
När du har täljare och nämnare som innehåller identiska faktorer kan du förkorta bort dessa. Om så inte är fallet kan vi vid vissa tillfällen själva skapa uttryck som är identiska, tex genom att faktorisera med konjugat och kvadreringsreglen.
Detta fungerar även då uttrycken endast skiljer sig på så vis att de har olika tecken. Genom att bryta ut en minusetta ur en av faktorerna kan du då skriva om dem till samma tecken. Följande kunskap är alltså användbar.
$\left(a-b\right)=\left(-1\right)\left(b-a\right)$(a−b)=(−1)(b−a)
Potensregler
För alla reella tal $m$m och $n$n och positiva tal $a$a och $b$b gäller att
$a^m\cdot a^n=a^{m+n}$am·an=am+n
$\frac{a^m}{a^n}$aman $=a^{m-n}$=am−n
$a^{-n}=$a−n= $\frac{1}{a^n}$1an där $a\ne0$a≠0
$(a^m)^n=a^{m\cdot n}$(am)n=am·n
$\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}$(ab )n=anbn
$(a\cdot b)^n=a^n\cdot b^n$(a·b)n=an·bn
$a^{\frac{1}{n}}=\sqrt[n]{a}$a1n =n√a
$a^0=1$a0=1
Kvadratrötter
$\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b}$√a·b=√a·√b
$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$√ab =√a√b
Polynomfunktioner
Andragradsfunktioner
Andragradsfunktionen är en av polynomfunktionerna. Här repeterar vi kort de olika begreppen.

Mer ingående förklaringar och övningsuppgifter hittar du i lektionen Vad är en andragradsfunktion?
Genom att flytta reglagen i sidled kan du undersöka hur konstanterna $a,\text{ }b$a, b och $c$c i andragradsfunktionen $f\left(x\right)=ax^2+bx+c$ƒ (x)=ax2+bx+c påverkar parabeln utseende.
Polynomfunktionens graf
Utifrån polynomfunktionens grad kan vi skissera grafens utseende. Skissen är grovt generaliserade, så tänk på att grafen till funktionerna varierar beroende på koefficienternas värden. Om exempelvis grafens derivata har sammanfallande rötter kan extrempunkter sammanfalla, vilket leder till att grafens utseende förändras.
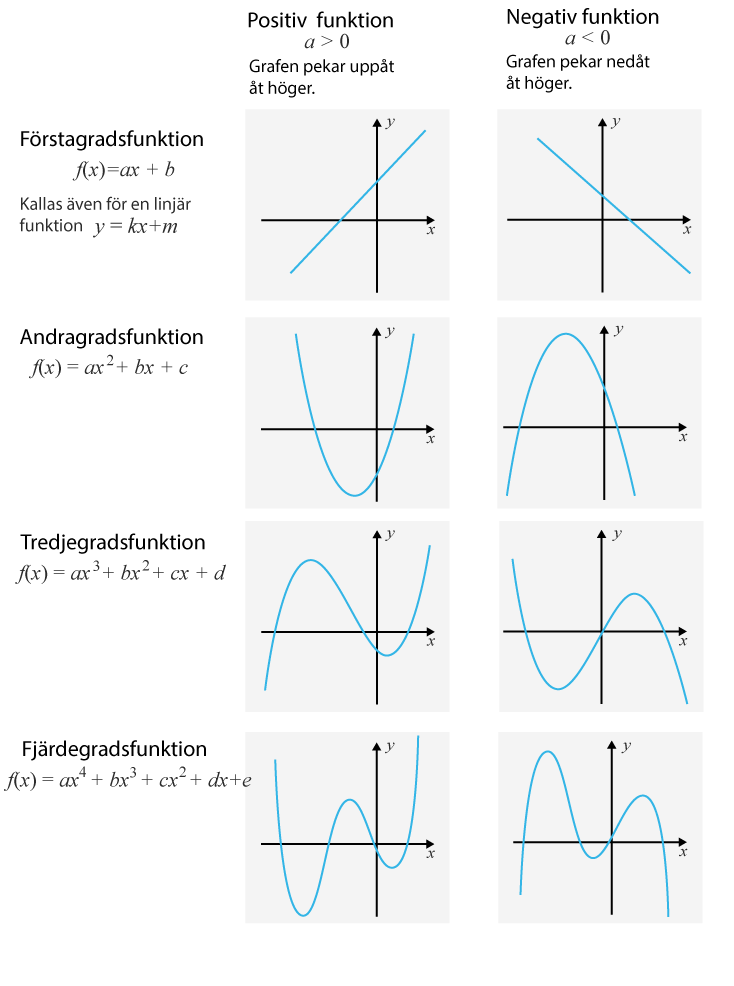
Några grundläggande minnesregel, som är mycket bristfälliga och grovt generaliserande, men ändå kan vara till hjälp, kan vara att
För udda gradtal börjar och slutar grafen åt olika riktning.
För jämna gradtal börjar och slutar grafen åt samma riktning.
De positiva polynomfunktionerna pekat uppåt längst åt höger.
De negativa polynomfunktionerna pekat nedåt längst åt höger.
Tips och vanliga fel vid ekvationslösning
Tänk på att aldrig dividera bort en variabel vid ekvationslösning. Du riskerar att förlora lösningar!
En ekvation har lika många lösningar som ekvationens gradtal, alltså polynomets största exponent för variabeln. Lösningarna kallas för rötter. Tex. andragradsekvationer kan ha två lösningar, tredjegradsekvationer tre och femtegradsekvationer fem lösningar. I vissa fall sammanfaller vissa lösningar, alltså en dubbelrot, trippelrot o.s.v.
När du löser en ekvation genom kvadrering kan även en så kallad falsk rot smyga sig med. Alltså en rot som inte ger likhet i ursprungsekvationen. Testa därför alltid dina rötter i den ursprungliga ekvationen när du kvadrerat.
Kontrollera även om det finns x-värden som inte är definierade. Vanligtvis är de odefinierade x-värdena de värden på $x$x som gör att nämnaren blir noll eller vid logaritmering, negativa $x$x-värden eftersom att $\lg a$lga bara är definierade för $a>0$a>0.
Fem sätt att lösa ekvationer på
1) Nollproduktmetoden – Denna metod är mycket användbar i denna kurs, eftersom att vi ofta ska ta fram derivatans nollställen. Har du termer vars summa är lika med noll så lär det vara denna metod som är mest effektiv!
3) Lösningsformeln även kallad PQ för andragradsekvationen
4) Grafisk lösning – Rita HL och VL som två olika funktioner och läs av skärningspunkternas $x$x-värden. De motsvarar ekvationens lösning. Finns inga skärningspunkter saknar ekvationen reella lösningar. I exemplet nedan söks lösningen till $f\left(x\right)=0$ƒ (x)=0, så kallade nollställen.
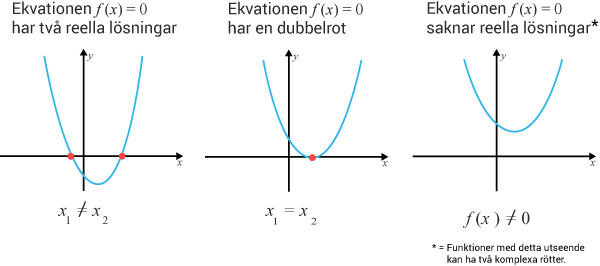
5) Logaritmer – Två vanliga baser är basen $10$10 och e. De har därför fått egna beteckningar.
$\log_{10}=\lg$log10=lg och $\log_e=\ln$loge=ln

Enligt logaritmlagar är
$10^x=y$10x=y $⇔$⇔ $x=\lg y$x=lgy
och
$e^x=b$ex=b $⇔$⇔ $x=\ln b$x=lnb.
En ekvation med variabeln i exponenten löser vi genom att ta logaritmen på båda leden.
Exempel
Lös ekvationen $2e^x=4$2ex=4
Lösning
$2e^x=4$2ex=4 dividera båda leden med två
$e^x=2$ex=2 logaritmera båda leden
$x=\ln2$x=ln2
eftersom att $\ln e^x=\ln b$lnex=lnb $⇔$⇔ $x\cdot\ln e=\ln b$x·lne=lnb $⇔$⇔ $x=\ln b$x=lnb
Vi kan läsa både $e^x=b$ex=b och $x=\ln b$x=lnb som
”Talet x är det tal som basen e ska upphöjas till för att svaret ska bli talet b.”
ln utläses som “det tal som basen e ska upphöjas till för att svaret ska bli…”
Ändringskvot/differenskvot, tangent och sekant
Genom att bestämma en sekant eller tangent kan vi uppskatta en funktions förändring.
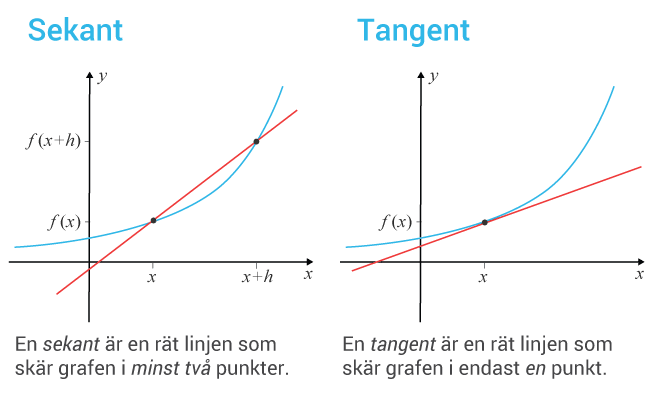
Sekanten ger förändringen i ett intervall. Tangenten ger förändringen i en punkt.

Den ändringskvot som ger bäst närmevärde vid numerisk beräkning är den centrala differenskvoten. Du väljer ett värde med samma avstånd framåt som bakåt i förhållande till punkten du ska bestämma ändringskvoten till och beräknar sedan
Genomsnittlig förändringshastighet $=\frac{\text{Förändringen i y-led}}{\text{Förändringen i x-led}}=\frac{\bigtriangleup y}{\bigtriangleup x}$=Förändringen i y-ledFörändringen i x-led =△y△x
Återvänd till lektionen om Genomsnittlig förändringshastighet och ändringskvoter för att repetera numeriska och grafiska ändringskvoter.
För att får ett bättre närmevärde på ändringskvoten väljs två punkter på funktionen med mycket litet avstånd till punkten vi vill beräkna förändringen i. Tex $h=\pm0,000\text{ }001$h=±0,000 001. Ju mindre avstånd, ju bättre värde. Men vill vi få ett exakt värde måste vi ha ett oändligt litet avstånd mellan punkterna. Vi behöver då räkna med gränsvärden.
Gränsvärde
Gränsvärdet inför vi för att kunna definiera derivatan algebraiskt.

För vissa uttryck och funktioner kan man beräkna gränsvärdet direkt genom insättning. För andra behöver man först förenkla eller skriva om uttrycket på olika vis, för att sedan kunna beräkna gränsvärdet.
Derivatans definition
Derivatans värde kan beskrivas som…
- kurvans lutning i en punkt, vilket är det samma som tangentens lutning i punkten.
- förändringshastigheten i en punkt på kurvan.
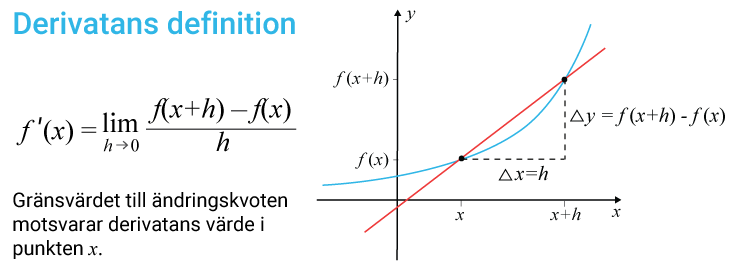
Exempel
Bestäm $f'(x)=2x^2+3$ƒ ’(x)=2x2+3 med derivatans definition
Lösning
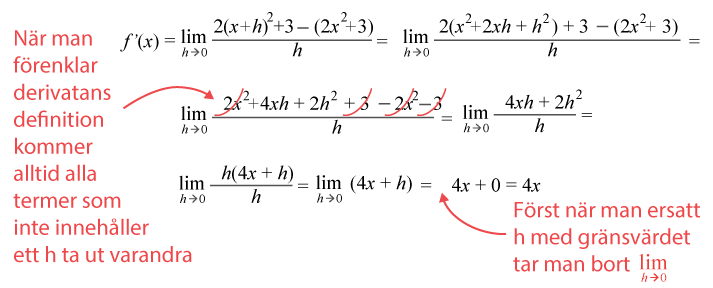
Deriveringsregler
Utifrån derivatans definition har man tagit fram deriveringsregler. Det finns två deriveringsregler. En för potensfunktioner och en för exponentialfunktioner.
TIPS
- Du deriverar alltid ett uttryck ”term för term”.
- Derivatan av en konstant är alltid lika med noll.
- Derivatan av en förstagradsterm är alltid lika med koefficienten.
- Om funktionen har variabeln i nämnaren eller under ett rottecken, så skriv om den i potensform för att sedan tillämpa deriveringsreglerna.
- Vi har inte lärt oss deriveringsregeln för produkter. Skriv om uttrycket till termer och derivata term för term.
Viktigt att komma ihåg att $a^0=1$a0=1

$\ln$ln står för den naturliga logaritmen, som är logaritmen med basen $e$e .
Därför är derivatan för exponentialfunktioner med basen $e$e extra lätt. Detta eftersom att $\ln e=1$lne=1 och vi får att derivatan är densamma som ursprungs funktionen om koefficienten i exponenten är lika med ett. Så fort du får $\ln e$lne så beräknar du det. Det ska inte finnas med i svaret.
Närmevärdet till talet $e\approx2,71828$e≈2,71828
Det är vanligt att man glömmer bort att det inte är korrekt att multiplicera en bas med en faktor.
Observera
$4\cdot3^2=4\cdot9=36$4·32=4·9=36 medan $\left(4\cdot3\right)^2=12^2=144$(4·3)2=122=144
På liknande sätt gäller att derivatan till $f\left(x\right)=3\cdot2^x$ƒ (x)=3·2x är lika med $f'(x)=3\cdot2^x\cdot\ln2$ƒ ’(x)=3·2x·ln2.
Men derivatan $f'(x)=3\cdot2^x\cdot\ln2\ne6^x\cdot\ln2$ƒ ’(x)=3·2x·ln2≠6x·ln2. Du kan inte heller förenkla derivatan till någon av följande då $f'(x)=3\cdot2^x\cdot\ln2\ne\ln12^x$ƒ ’(x)=3·2x·ln2≠ln12x och $f'(x)=3\cdot2^x\cdot\ln2\ne\ln6\cdot2^x$ƒ ’(x)=3·2x·ln2≠ln6·2x
Du får alltså INTE multiplicera basen med faktorn $k$k eller $\ln a$lna i $f´(x)=C\cdot a^{kx}\cdot\ln a$ƒ ´(x)=C·akx·lna
Derivatan och tangentens lutning
Växande och avtagande
Med derivatan kan vi analysera funktionens utseende och egenskaper.
När funktionen är växande är derivatan positiv och alla tangenter i intervallet har en positiv lutning.
När funktionen är avtagande är derivatan negativ och alla tangenter i intervallet har en negativ lutning.
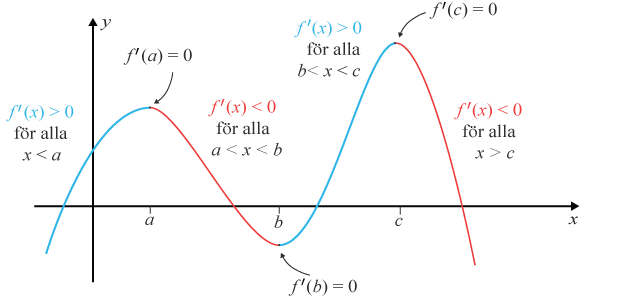
Bestäm extrempunktens karaktär
I extrempunkterna är $f'(x)=0$ƒ ’(x)=0 . I dessa punkter hittar du lokala och eventuellt globala max och minimipunkter. Alla extrempunkter kan verifieras med antingen med
1) Teckentabell
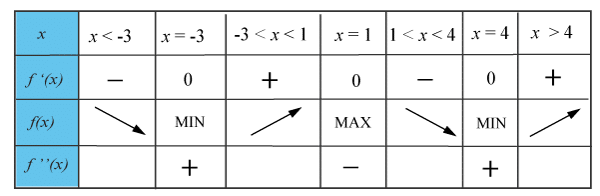
$f”(x)<0$ƒ ”(x)<0 ger att punkten där $x=a$x=a är en maximipunkt
$f”(x)>0$ƒ ”(x)>0 ger att punkten där $x=b$x=b är en minimipunkt
3) Skissa och resonera kring kurvans egenskaper.
Tänk då på att det är funktionen och inte derivatans graf du ska föra ditt resonemang kring.
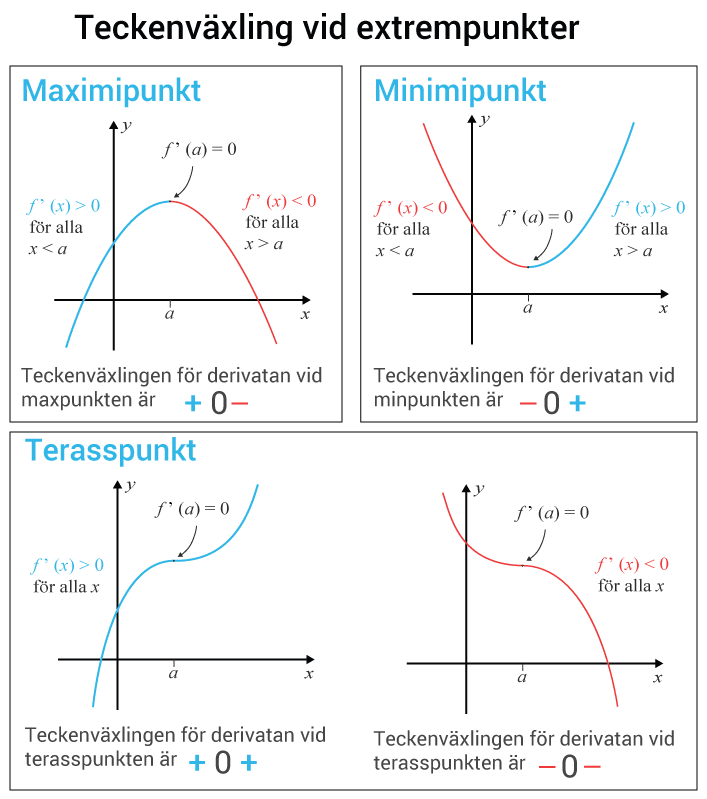
$f(x)$ƒ (x) har en extrempunkt då $f'(x)=0$ƒ ’(x)=0
$f´(x)=0$ƒ ´(x)=0 ger en maximipunkt då $f”(x)<0$ƒ ”(x)<0
$f´(x)=0$ƒ ´(x)=0 ger en minimipunkt då $f”(x)>0$ƒ ”(x)>0
Då $f´(x)=0$ƒ ´(x)=0 ger att $f”(x)=0$ƒ ”(x)=0 måste karaktären bestämmas med en teckentabell.
Teckentabell
I teckentabellen får du en bild av grafens utseende.
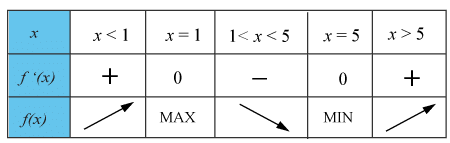
I tabellen kan du läsa av extrempunkterna, deras karaktär och om funktioner är växande eller avtagande mellan dem.
Genom att beräkna fram $y$y-koordinaterna för extrempunkterna kan du göra en ännu bättre skiss. Det gör du genom att sätta in $x$x-värdena i funktionsuttrycket. Du kan med fördel även bestämma var kurvan skär $y$y-axeln. Punktens $y$y-värde motsvarar alltid konstanttermen i uttrycket, eftersom att att $x=0$x=0 i denna punkt. Du kan även bestämma funktionens nollställen, alltså där grafen skär $x$x-axeln, där $f\left(x\right)=0$ƒ (x)=0 eller någon annan valfri punkt på grafen för att få en ännu noggrannare skiss.
Primitiva funktioner och integraler
Funktionen $F\left(x\right)$F(x) är en primitiv funktion till funktionen $f\left(x\right)$ƒ (x) om
$F'(x)=f\left(x\right)$F’(x)=ƒ (x)
Alltså om den primitiva funktionen $F:s$F:s derivata är lika med funktionen $f$ƒ .
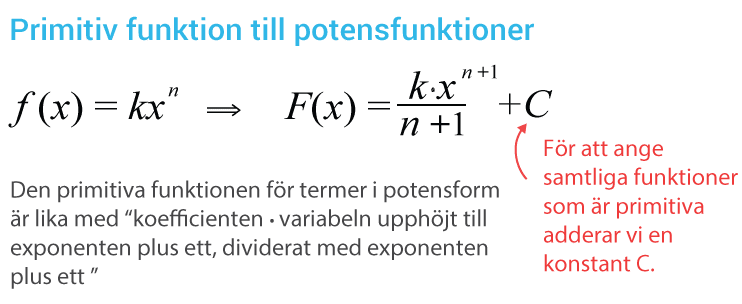

Men hjälp av en punkt på grafen kan man bestämma konstanten $C$C. Har du ingen punkt kan du ta fram en genom att sätta in ett värde på $x$x som ingår i definitionsmängden och beräkna funktionsvärdet $f\left(x\right)$ƒ (x) och på så sätt få punkten $\left(x,\text{ }f\left(x\right)\right)$(x, ƒ (x)).
Integraler
Integraler kan förenklat beskrivas som en summa av alla förändringar i ett intervall.
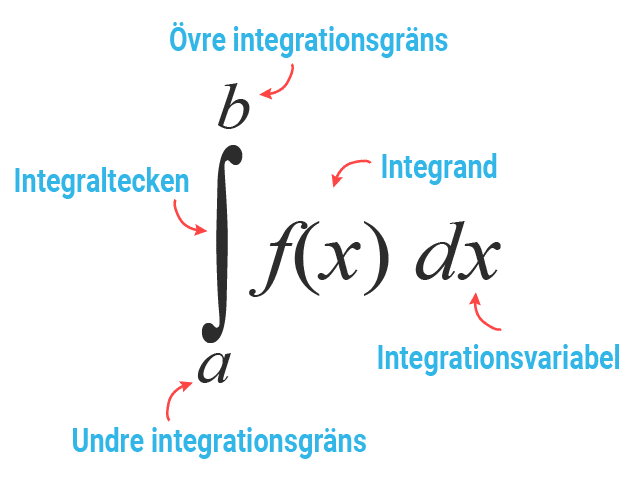
Ett vanligt sätt att bestämma integralens värde är att beräkna arean mellan en funktions kurva och $x$x-axeln i ett intervall.
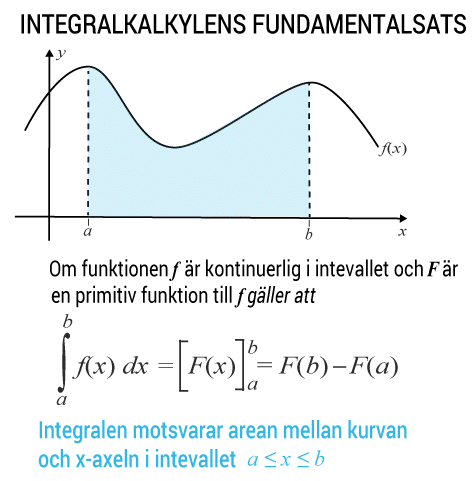
Var noga med att få rätt på alla tecken när du beräknar integralen! Ett tips kan vara att behålla parentesen och beräkna värdet i varje parentes innan subtraktionen $F\left(b\right)-F\left(a\right)$F(b)−F(a) utförs.
I lektionen Tillämpning av integraler kan du repeterar sambandet mellan integralen och integranden.
Geometriska talföljder
En följd av tal, där kvoten $k$k mellan två på varandra följande tal är konstant hela talföljden, kallas för en geometrisk talföljd. Talen i talföljden kallas också för element. Det första talet i talföljden betecknas $a_1$a1.

Kvoten $k$k beräknas med formeln $k=$k= $\frac{a_{n+1}}{a_n}$an+1an
Man kan bestämma det $n$n:te elementet i talföljden med formeln $a_n=a_1\cdot k^{n-1}$an=a1·kn−1
För att beräkna en summa av upprepade förändringar, tex hur mycket pengar man har på ett konto efter ett antal lika stora insättningar på ett konto med en konstant ränta, kan man med fördel ta vara på att dessa händelser kan beskrivas matematiskt som summan av en geometrisk talföljd.
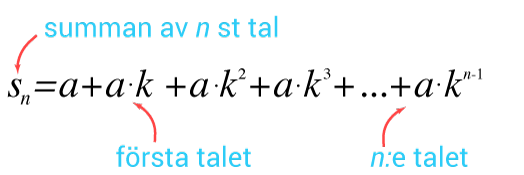
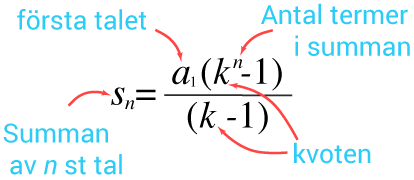
Då talföljden innehåller många termer blir det mycket effektivt att använda sig av formeln för den geometriska summan. Den kan förenklat skriva om på detta sätt.
Linjär optimering
Linjär optimering som en metod för att hitta ett så optimalt, värde som möjligt utifrån ett antal olika villkor.
Alla punkter i området kommer att klara alla begränsningar, uppfylla alla villkor, och därmed vara värden som är möjliga utifrån villkoren. Med linjär optimering möjliggör vi att inte bara hitta alla möjliga, utan även det bästa värdet.
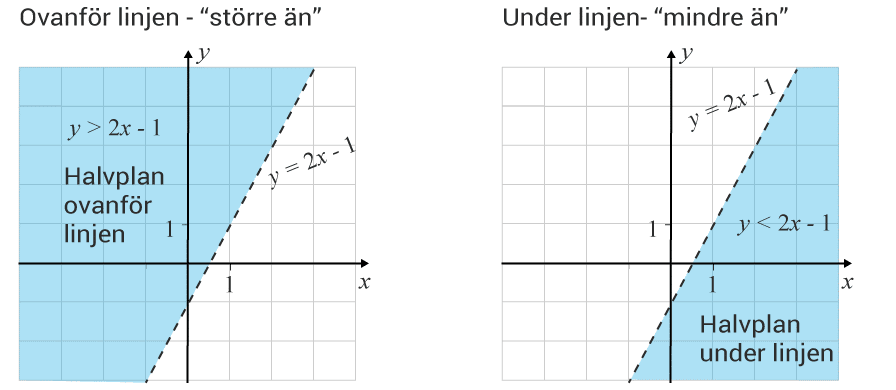
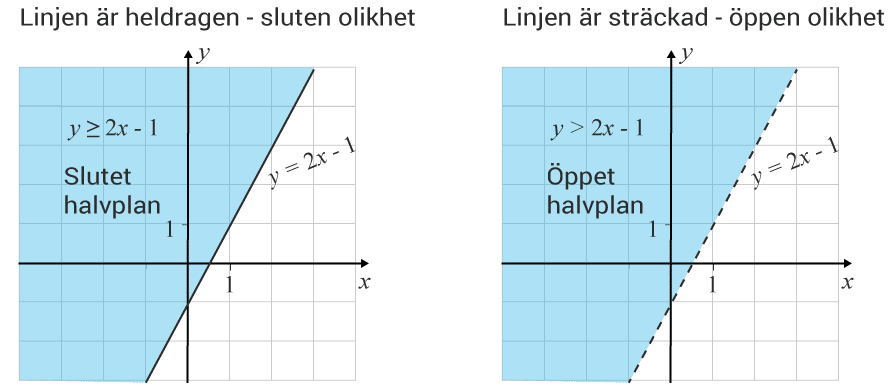
Den funktion $m(x,y)=ax+by$m(x,y)=ax+by som ger möjlighet att beräkna det man vill optimera när man löser ett optimeringsproblem kallas för en målfunktion. Genom att teckna villkoren som linjära olikheter och rita in i samma koordinatsystem, kan vi hitta det optimala värdet genom att sätt in koordinaterna för områdets hörnpunkter i målfunktionen.
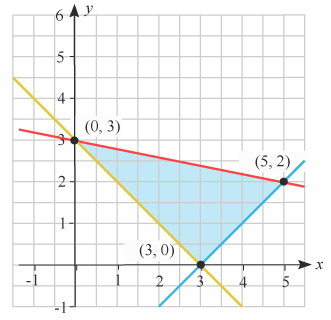
Målfunktionen ritas inte in i koordinatsystemet utan bara de funktioner som motsvarar villkoren. Tänk på att teckna dessa med samma variabel.
Repetitionsmaterial
Tyvärr kommer du inte att få tillgång till all information som delas här, i sammanfattning Matematik 3b, vid Nationella provet.
Använd gärna några av våra kapiteltest för att repetera och fördjupa dina kunskaper. Samtliga uppgifter har fullständiga förklaringar.
Aritmetik, Polynom och Rationella uttryck Ma3b
Grundläggande maximi och minimiproblem Ma3b
Derivatan och grafen Ma3b
Primitiva funktioner och Integraler Ma3b
Linjär optimering Ma3b
Geometriska talföljder Ma3b
Här kan du hitta alla gamla nationella prov att öva på.![]()

Endast Premium-användare kan kommentera.