
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Fysik 1
/ Krafter
Friläggning, vektorer och skalärer
Friläggning
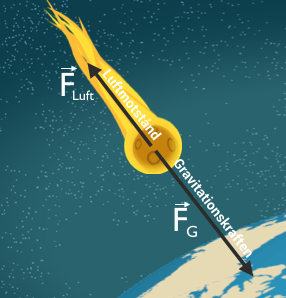
Att måla upp ett fysikaliskt problem och sätta ut alla krafter i form av pilar ger oss en överskådlig bild av problemet. Detta kallas för att frilägga problemet. Vanligtvis väljer man att kalla de olika krafterna för F, som kommer från det engelska ordet ’Force’. För att visa att en variabel är en kraft så sätter vi också en lite pil över bokstaven.
I fallet med en meteor ser friläggningen ut enligt följande:
Vektorer
I matematiken kallar man objekt med både storlek och riktning för vektorer. Ett vanligt sätt att beskriva vektorer är genom att sätta in dem i ett koordinatsystem. En kraft kan då beskrivas i form av vilken x- samt y-koordinat som den pekar på (när den startar i origo).
Inom fysiken finns det flera storheter som faller inom gruppen vektorer. Andra exempel än kraft är: hastighet och acceleration.
Skalärer
Storheter som har en storlek men ingen riktning kallas för skalärer. Ett exempel på en skalär storhet är massan hos ett föremål.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (4)
-
1. Premium
Att frilägga innebär att…
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
2. Premium
En kraft är ett exempel på en storhet som faller under kategorin…
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
3. Premium
En hastighet är ett exempel på en storhet som faller under kategorin…
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
4. Premium
Vilken av följande storheter är exempel på en skalärstorhet?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...

Endast Premium-användare kan kommentera.