
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 5
/ Derivata och Integraler – Ma 5
Förändringshastigheter och Derivata - Kedjeregeln
Innehåll
Vissa händelseförlopp beskrivs bäst med en matematisk modell som är en sammanslagning av fler olika funktioner. Dessa funktioner kallas för sammansatta funktioner och består av så kallade inre och yttre funktioner. När dessa deriveras används kedjeregeln.
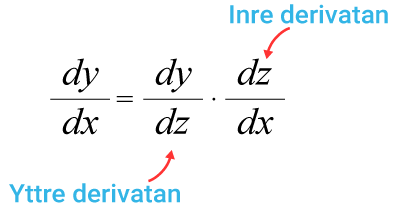
För att tydligare se sambanden mellan olika variabler och förändringshastigheter i de sammansatta funktionerna kan man med fördel använda följande skrivsätt.
Om ballongens area ökar med tiden, så kommer så klart även ballongens volym att öka. Hur kan vi använda sambandet mellan förändringen av volymen och radien beroende av hur långtid vi har fyllt ballongen med luft?
Mer om det senare.
Förändringshastigheter och derivata
Beräkningarna nedan bygger på kunskap som vi gått igenom i tidigare lektioner. Återvänd till dem om du känner dig osäker på följande.
Sammansatta funktioner
Funktionen $ y = f(g(x)) $ är en sammansatt funktion där $f(g(x))$ är den yttre funktionen och $g(x)$ är den inre funktionen.
En sammansatt funktion kan även skrivas med tecknet ∘, en mittplacerad ring som uttalas ”boll”.
$f\text{ }\text{∘}\text{ }g\left(x\right)=f\left(g\left(x\right)\right)$ƒ ∘ g(x)=ƒ (g(x))
Kedjeregeln
Derivatan av en sammansatt funktion ges av kedjeregeln vilken säger att
$ y´= f´(g(x))⋅g´(x) $
där
$ f´(g(x)) $ kallas den yttre derivatan och $g´(x)$ den inre derivatan.
Olika sätt att beskriva derivata
När vi tillämpar kedjeregeln är det viktigt att veta vilken variabel som vi deriverar med avseende på. Därför behöver vi förtydliga sättet vi beskriver derivatan.
Om vi till exempel har ett klot vars radie ökar med avseende på tiden, ökar indirekt även volymen på klotet med tiden. Volymen beror av radien $r$r som i sin tur beror av tiden $t$t. Om vi deriverar funktionsuttrycket som beskriver volymen, får vi då förändringshastigheten med avseende på radien eller volymen?
Vi introducerar ett nytt skriv sätt.
Klotets volym $V=$V=$\frac{4\pi r^3}{3}$4πr33 förändras med avseende på radien där radien $r$r förändras med avseende på tiden $t$t på så sätt att radien blir dubbel så stor var minut. Radien kan alltså beskrivas som en funktion av tiden $r\left(t\right)=2t$r(t)=2t.
Förändringshastigheten för volymen $V´\left(t\right)$V´(t) med avseende på tiden $t$t kan även skrivas som $\frac{dV}{dt}$dVdt , vilket kan läsas som ”derivatan av $V$V med avseende på variabeln $t$t ”. När vi deriverar denna funktion ser vi alla andra variabler än $t$t som konstanter och behandlar dem som detta. Kvoten $\frac{dV}{dt}$dVdt ger då förhållandet mellan dessa förändringar, det vi kallar ändringskvoten eller förändringhastigheten.
Denna förändringshastighet delas nu upp i två steg.
Förändringshastigheten för klotets volym $V´\left(r\right)$V´(r) med avseende på radien $r$r kan skrivas som $\frac{dV}{dr}$dVdr och är lika med $4\pi r^2$4πr2.
Och förändringshastigheten för klotets radie $r´\left(t\right)$r´(t) med avseende på tiden $t$t kan skrivas som $\frac{dr}{dt}$drdt och är lika med $2$2, alltså dubbel så stor var minut.
Vi kan beskriva volymens förändringshastighet med avseende på tiden med hjälp av kedjeregeln, där volymen med avseende på radien är den yttre funktionen och radien med avseende på tiden den inre.
$\frac{dV}{dt}=\frac{dV}{dr}\cdot\frac{dr}{dt}$dVdt =dVdr ·drdt
och teckna derivatan som
$\frac{dV}{dt}=$dVdt = $4\pi r^2\cdot2=8\pi r^2$4πr2·2=8πr2
Detta kan du nu använda för att bestämma radiens och volymens förndringshastigheter vid olika tidpunkter.
Tillämpning av Kedjeregeln
Om sidan för en kub ökar med tiden så kommer volymen för kuben förstås även den att öka. Vi kan då säga följande om sambandet mellan volymens ökning med tiden och sidans ökning:
Volymen beror av hur lång sidan är och beräknas med hjälp av $ V = s^3 $.
Sidan beror på tiden så vi kan säga att det finns en inre funktion $ s(t) $ och volymen kan då beskrivas med $ V = (s(t))^3 $.
Vi kan då ställa upp sambandet
$\frac{dV}{dt}=\frac{dV}{ds}\cdot\frac{ds}{dt}$dVdt =dVds ·dsdt
Dvs att Förändringshastigheten av volymen med avseende på tiden är lika med förändringshastigheten av volymen med avseende på sidan som i sin tur har en inre funktion. Denna inre funktion är förändringshastigheten av sidan med avseende på tiden.
Exempel 1
Volymen för en kub minskar i ett tidsintervall med $ 8 \, m^3 / h$. Bestäm hur snabbt sidan $s$ minskar då denna vid en tidpunkt är $ 10 m $.
Lösning
Här vet vi att $ \frac{dV}{dt} = -8 \, m^3/h $.
$ \frac{dV}{ds} = 3s^2 $ och sätter vi in $ s=10\,m $ får vi $ \frac{dV}{ds} = 300 $.
Vi kan då ställa upp sambandet
$ \frac{dV}{dt} = \frac{dV}{ds}⋅\frac{ds}{dt} ⇔ $
$ -8 = 300⋅\frac{ds}{dt} ⇔ $
$ \frac{ds}{dt} = \frac{-8}{300} ≈ -0,0266$
Alltså gäller att sidan minskar med $ 0,0266 \, m/h $
När vi deriverar sammansatta funktioner med kedjeregeln ser vi alla andra variabler än den variabel du deriverar med avseende på som konstanter och behandlar dem som detta.
Exempel i videon
- Beskrivning av ett samband för att förstå förändringshastigheten av volymen för en sfär vid en viss tidpunkt.
- När volymen för en digital kub växer så ökar sidan s med 2 cm/sekund. Med vilken hastighet ökar volymen då sidan är 12 cm?
- Volymen för en sfärisk ballong ökar vid en tidpunkt med 24 cm³/s. Hur snabbt ökar radien då denna är 20 cm vid tidpunkten?
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (5)
-
1. Premium
$ T = 16ab + a^2 + 2 $. Bestäm $ \frac{dT}{da} $
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
2. Premium
Volymen för en cylinder beräknas med hjälp av $ V = \pi r^2⋅h $ där $ r=radie $ och $ h=höjd $. Bestäm derivatan av volymen med avseende på höjden.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
3. Premium
Bestäm $\frac{dy}{dx}$ då $ y= 3sin(3x) $ med hjälp av kedjeregeln.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
4. Premium
Förändringen av volymen för en sfär som ändras med tiden kan beskrivas med sambandet $ \frac{dV}{dt} = \frac{dV}{dr}⋅\frac{dr}{dt} $ Ange vilket alternativ som beskriver $\frac{dr}{dt}$.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
5. Premium
Karl-Johan skall bestämma $\frac{dy}{dt}$ då $ y=e^t⋅sin(2x) $. Han skriver sin lösning på följande vis:
$ y´ = e^t⋅sin(2x) + e^t⋅cos(2x)⋅2 = $ $ e^t(sin(2x)+2cos(2x)) $
Vad gör han fel?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...
c-uppgifter (2)
-
6. Premium

En kub har sidor med längden $ a \, cm $ och en volym som vi kallar för $ V $. Kubens volym ökar med $ 20 \, cm^3/s $. Bestäm hur snabbt längden $ a $ ökar då kantlängden är $ 5 \, cm $.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
7. Premium

Volymen för en kon kan beräknas med formeln $ V=\frac{\pi⋅r^2⋅h}{3} $. Bestäm hur mycket volymen för en kon ökar när höjden är $10\,cm$ och ökar med $ 0,50 \, cm/s $. Radien är $2,0\,cm$ och förändras inte.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...
a-uppgifter (1)
-
8. Premium
En stor klotformad ballong läcker ut luft, så att volymen minskar med en hastighet som är proportionell mot begränsningsarean. Ballongen behåller sin klotform.
Vilket påstående är korrekt?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...

Nils Nyberg
Hej!
Grym hemsida! Det var ett tag sedan jag gick i gymnasiet och jag undrar varför enheterna omvandlas från centimeter/sekund till (kubik)centimeter/sekund osv.
Anna Eddler Redaktör (Moderator)
Hej Nils,
kul att Eddler kan hjälpa dig.
Kolla in denna lektion där teoritexten nämner lite om derivatans enheter.
Problemlösning med Derivatan
Grillska gymnasiet Uppsala
I avsnittet Olika sätt att beskriva derivata ska det stå
dy/da=4b inte 4ab som det står nu.
För övrigt har jag stor nytta av era genomgångar!
/Anders,
Simon Rybrand (Moderator)
Kul att du gillar genomgångarna!
Texten är fixad, tack för att du sade till!
adriankd@kth.se
Fråga 5 innehåller fel. Volymen ökar med 20 cm^3 inte 20cm^2.
När a = 5 blir dv/da = 3*5^2= 75 , inte 50 som det står i lösningen.
Simon Rybrand (Moderator)
Hej
Tack för att du sade till om detta, det är korrigerat i uppgiften!
Pauline Mengel
Hejsan, det verkar som svaret fortfarande är fel, det står fortfarande att att 3*5^2=50 och inte 75.
Simon Rybrand (Moderator)
Hej
Ja det verkar vi ha missat att ändra konstigt nog. Nu skall det dock vara fixat!
Endast Premium-användare kan kommentera.