
Vad är korsmultiplikation och när används det?
2019-03-15 Av Simon Rybrand 0 kommentarer
Kanske har du hört eller läst raden ”Nu använder vi korsmultiplikation och får…”? Sedan funderar du på vad som egentligen hände med uttrycket. Här tänkte jag att vi reder ut när och varför det används och hur det går till steg för steg.
När och varför används korsmultiplikation?
Korsmultiplikation är en teknik som används framförallt vid ekvationslösning och när man skriver om formler (lösa ut formler). Anledningen till att man använder det är för att det är en smidig teknik när ekvationerna innehåller bråkuttryck. Det kan vara uttryck som ser ut på följande vis.
$\frac{x}{4}=\frac{5}{2}$x4 =52
Här ovan har du en ekvation där både vänsterledet och högerledet är bråkuttryck (rationella uttryck). Sådana ekvationer uppstår exempelvis ofta när du jobbar med likformighet.
När ekvationen eller formeln ser ut på det här sättet så är en smidig teknik att korsmultiplicera för att lösa ekvationen. Så hur går detta till?
Så går det till – steg för steg
Korsmultiplikation
När du korsmultiplicerar en ekvation så
- Multiplicerar du vänsterledets nämnare med vänsterledet och högerledet samt högerledets nämnare med vänsterledet och högerledet.
- På det viset ”blir du av med” (mer om vad som händer nedan) bråkuttrycken.
För att göra detta lite tydligare är det enklare att visa ett exempel där vi korsmultiplicerar steg för steg för att lösa ekvationen $\frac{x}{4}=\frac{5}{2}$x4 =52 .
Steg 1 – Korsmultiplicera
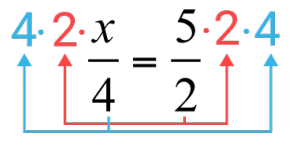
Vi börjar med att multiplicera vänsterledets nämnare $4$4 med vänsterledet och högerledet.
Vi multiplicerar även högerledets nämnare $2$2 med vänsterledet och högerledet.
Här vill jag också nämna att det kan vara lite förvirrande att ordet korsmultiplikation används. Vi multiplicerar ju inte direkt alla termer kors och tvärs i ett kors 😉 Så det kan vara bra att granska bilden här ovan noggrant för att det skall blir tydligare.
Steg 2 – Förkorta
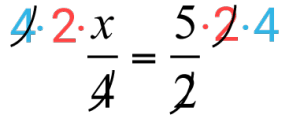
Nu kan vi förkorta vänsterledet med $4$4 och högerledet med $2$2. Då ”blir vi av med” nämnarna. Det som händer där är att vi i vänsterledet har $\frac{4}{4}=1$44 =1 och i högerledet har vi $\frac{2}{2}=1$22 =1.
På det viset får vi $1\cdot2\cdot x=2x$1·2·x=2x i vänsterledet och $5\cdot1\cdot4=20$5·1·4=20 i högerledet.
Så på det här viset får vi kvar
$2x=20$2x=20
Steg 3 – Lös klart ekvationen
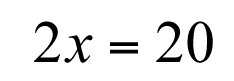
För att slutligen lösa ut $x$x så kan vi dela bägge leden med $2$2.
$\frac{2x}{2}=\frac{20}{2}$2x2 =202
$x=10$x=10
Här ovan så visar jag alla steg väldigt noggrant och det brukar man vanligtvis inte göra. Om du har bra koll på metoden så brukar man gå från steg 1 till steg 3 direkt och bara skriva att man korsmultiplicerar. Det skulle exempelvis kunna se ut på följande vis.
Lös ekvationen $\frac{4x}{5}=\frac{5}{7}$4x5 =57
Lösning
Korsmultiplikation ger (Testa gärna själv)
$28x=25$28x=25 Dela med 28
$x=\frac{25}{28}\approx0,89$x=2528 ≈0,89
Här hoppas jag nu att du som har funderat på vad korsmultiplikation är har fått ett bra svar. Om du har några frågor så går det bra att ställa dem i kommentarerna här nedan.

Med vänlig hälsning
Simon Rybrand