
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Högskoleprovet matematik
/ Övningsprov och förslag lösningar
XYZ – del1

Här kan du testa dig själv på ett gammalt högskoleprov på delen XYZ. Provet är från den kvantitativa delen hösten 2011.
Till den här lektionen är det endast övningsuppgifter och ingen video. Du startar övningarna genom knappen ”starta”.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (12)
-
1. Premium
Vilket av följande tal är störst om x är ett negativt heltal?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
2. Premium
Vad är $ \frac{1}{ \frac{1}{x} + \frac{1}{2} } $ om x = 4?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
3. Premium
Vad är 50 promille av en femtiondels miljon?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
4. Premium
ABCD är en parallellogram där vinkeln C är 2x grader och vinkeln D är 3x grader. Vad är x?
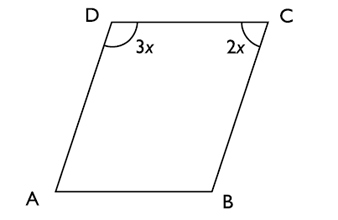 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
5. Premium
Antag att y = x(1+x) där x är ett positivt heltal. Vilket svarsförslag är ett möjligt värde på y?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
6. Premium
Vilket svarsförslag är lika med $ \sqrt{50} $?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
7. Premium
Vad är xy om $ \frac{ \frac{3}{x} }{ \frac{y}{7} } = 1 $?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
8. Premium
Vilket av följande påståenden är korrekt?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
9. Premium
Sannolikheten att slumpmässigt dra ett visst kort från en kortlek är P. Hur många kort är det i kortleken?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
10. Premium
Vilka av punkterna P, Q, R och S ligger på linjen 3x + 4y = 0?
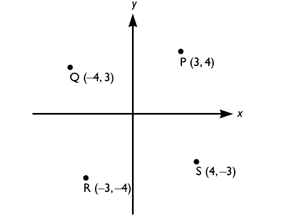 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
11. Premium
Vilket svarsförslag kan vara mindre än 0 om x > 0, y > 0 och z < 0?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
12. Premium
Trianglarna T1 och T2 är likformiga. Arean av T1 är 72 cm². Vilken area har T2?
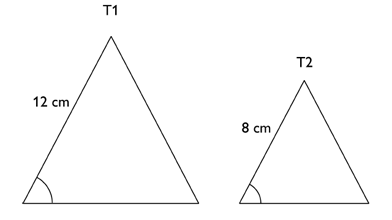 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar...

Radman Tahmasebi
Många av metoderna som används för att komma fram till rätt svar är alldeles för tidskrävande. Den här typen av uppgift har man cirka 1 minut på sig att lösa på högskoleprovet. Ett exempel är uppgift tio. Istället för att ”testa varje punkt tills du får rätt svar” kan man utesluta två av de alternativen som innehåller P eftersom att både x och y koordinaten är positiva och att addera två positiva tal kommer ge oss ett positivt resultat och inte noll. När svaren på de här frågorna är formulerade på det här sättet ger det tyvärr inte mycket hjälp med den ”listighet” som krävs på högskoleprovet.
Simon Rybrand (Moderator)
Hej
Håller med om detta och tanken med genomgångarna är inte alltid att erbjuda vägen till det snabbaste svaret utan att man skall sakta men säkert träna in hur olika typer av uppgifter kan lösas samt vilken matematik som ligger bakom dessa.
Däremot är det en bra idé att kanske även visa på hur man snabbt kan lösa uppgifter som ett alternativ.
Karl
Hej! Denna fråga är från höstens högskoleprov, provpass 5, fråga 2.
5^33 är ett heltal. Vilken entalssiffra har heltalet?
A: 0
B: 1
C: 5
D: 9
Hur kan man räkna ut denna typ av fråga??
Simon Rybrand (Moderator)
Hej
Det borde vara entalssiffran 5.
$5^2=5·5=25$
$5^3=5·5·5=125$
$5^4=5·5·5·5=625$
…
Man kan även visa detta genom att räkna med kongruensräkning mod 10. Säg till om du vill att jag skall visa det också!
Arsema Kifle
tack sa mycket, det hjalpte!
Arsema Kifle
hej, kan du forklara fraga 9 pa ett annat satt?
tack pa forhand!
Simon Rybrand (Moderator)
Hej
Jag har fyllt på förklaringen till den uppgiften ganska mycket.
Kika på det och säg till om du vill diskutera vidare den!
natalie mirzayi
Hej fråga 11 förstår jag inte alls, kan du förklara lite tydligare ?
Simon Rybrand (Moderator)
Hej
Jag har uppdaterat förklaringen till den uppgiften med ett förtydligande så att det ska vara enklare att se vilket alternativ som kan vara mindre än noll.
Hoppas att detta hjälpa dig att förstå denna uppgift!
Samuel Bahta
Tack Simon, lätt följa och förstå bra material … 🙂
ida
Hej.
På fråga tolv så hänger jag inte med på detta
4/9=x/72 och sedan löser dom ut x så att det blir x=(72×4)/9
Hur kommer det sig att man kan lösa ut x på det viset? Vilka regler gäller?
Simon Rybrand (Moderator)
Hej, jag kan göra så att jag skriver ut några steg till här i den ekvationslösningen:
$ \frac{4}{9} = \frac{x}{72} $
Multiplicera bägge sidor i ekvationen med 72 så att du får
$ \frac{72*4}{9} = \frac{72*x}{72} $
I högerledet blir vi av med 72 i nämnaren nu då 72/72 = 1 och vi får
$ \frac{72*4}{9} = x $
annelie.b
Hej!
Förstår inte förklaringen till svaret här nedan. Hur ska man veta att ”Det innebär att du multplicerar ett heltal med det närmast efterföljande heltalet” – vilka regler gäller här? Hur ska man tänka? Tack på förhand. /Annelie
Fråga 5
”Antag att y = x(1+x) där x är ett positivt heltal. Vilket svarsförslag är ett möjligt värde på y? Du svarade tyvärr fel
Ditt svar:
Rätt Svar: 20
Förklaring
Här multipliceras x med x+1. Det innebär att du multplicerar ett heltal med det närmast efterföljande heltalet, tex:
1⋅2=2
2⋅3=6
3⋅4=12
4⋅5=20
Rätt svar är 20.”
Simon Rybrand (Moderator)
Hej, här får du i frågeställningen reda på att x är ett positivt heltal. Dvs x är något av talen
1, 2, 3, 4, 5, 6, … osv
Då måste x+1 vara det närmast följande talet efter x, så om x = 2 så är x +1 = 2+1= 3.
Eftersom svarsförslagen är relativt små och ligger nära varandra så gör vi så här att vi testar olika värden på x med start från x = 1.
När vi har kommit till x = 4 och detta ger att
x + 1 = 5 så får vi x(x+1) = 4*5 = 20 så ser vi att detta är ett av svarsalternativen. Vi kan då svara just detta.
johannawallstrom
Hej!
Alltså fråga 12, hur kommer jag fram till 4/9 av 64/144??
Är helt uttömd
Tack för bra materiel!
Simon Rybrand (Moderator)
Hej, det du behöver göra är att förkorta det tills du får fram 4/9, ett förslag för att göra detta utan räknare är att förkorta med 2 i täljare och nämnare tills du inte kan förkorta mer:
$ \frac{64/2}{144/2} = \frac{32}{72} = \frac{32/2}{72/2} = $
$ \frac{16}{36} = \frac{16/2}{36/2} = \frac{8}{18} = \frac{8/2}{18/2} = \frac{4}{9} $
fiaia
Snälla rara, kan du inte förstora upp bilderna lite, det är galet svårt att se, speciellt x y och z i talen?
Simon Rybrand (Moderator)
Hej, jag har förstorat upp (framförallt i förklaringarna) de delar som jag tror blir lite små i textstorleken i detta test. Hoppas att det hjälper, annars är det bara att hojta till här igen så förstorar vi det ännu mer.
Milan
Hej!
I uppgift 12 står det att trianglarna är likformiga, men det står ingenting om att de är liksidiga. Så därför kan man inte anta att även basen är 12cm lång eller hur? Den kan väl lika gärna vara 13 o höjden 11.077?
Simon Rybrand (Moderator)
Hej Milan, håller med dig helt och vi ändrar i denna uppgift, det är helt klart bättre att använda sig av att förhållandet mellan trianglarna är likformigt.
BotenAnnie
fråga 11 .. kan du förklara varför resten alltid blir positivt? jag kan inte se sambanden där hur du tänker.
Simon Rybrand (Moderator)
Det är bra att tänka i termer av vilka tal som egentligen är positiva alternativt negativa. Vi vet följande:
z < 0 (negativt) x > 0 (positivt)
y > 0 (positivt)
Så om vi går igenom varje rationellt uttryck för sig:
$ \frac{y-z}{x} $
Här är y – z positivt för att (+y) – (-z) = y + z > 0
$ \frac{xz}{xyz} $
Här får du i täljaren negativt för att (+x)*(-z) är negativt. Likadant i nämnaren. MEN när dessa divideras får du ett positivt svar då division med två negativa tal ger positivt svar.
$ \frac{ \frac{z}{y} }{ \frac{z}{x} } $
Samma resonemang som nummer 2
Alwisw
Hej!
Nu tänker jag vara lite besvärlig och kommentera 3 av uppgifterna.
På 6:an tänkte jag att roten ur 50 låg närmast roten ur 49 – ett tal jag kan med huvudräkning. Och efter beräkning låg 5√2 helt enkelt närmast. Är detta ett hållbart sätt att tänka?
På 10:an löste jag ut y ur ekvationen och gjorde om formeln till y=kx+m och fick då att y=-3/4 x och drog slutsatsen att linjen inte skär y-axeln i någon punkt och tänkte då att Q och R ligger på linjen. Detta visade sig vara helt fel. Man ska alltså inte lösa ut y, eller har jag missförstått att det här y=-3/4x Inte betyder att linjen inte skär y-axeln?
Till sist – 12:an: Här tänkte jag att för stora triangeln beräknas arean: 12xb/2 = 72 cm vilket ger att b=12 och att man då p.g.a likformigheten kan beräkna basen på lilla triangeln med 12 x 8/12 = 8 vilket sen ger att 8×8/2=32 cm2. Hade jag bara tur att detta ledde fram till rätt resultat eller kan man tänka såhär? Verkade som att förklaringen ni gav var mycket smidigare.
Ed
Jag har inget med den här sidan att göra men tänkte att jag kunde försöka svara dig så gott det går ändå.
Visst kan det vara hållbart att tänka så men jag skulle uppmana att tänka så här istället: √50=√(25*2)=5√2 då √25=2. Hoppas du förstod tankegången.
När jag löste uppgift 10 gjorde jag likadant och fick att y=-3x/4. Du säger att den inte skär y-axeln vilket är fel. Räta linjens ekvation säger att y=kx+m där m är skärningspunkten på y-axeln. I vårt fall, uppg 10, har vi ett värde på m som är 0. Dvs den skär i origo och därför blir svaret Q och S.
På uppg 12 kan du resonera på båda sätten.
Littleprincess
Finns inte dom här talen som genomgång?
Simon Rybrand (Moderator)
Hej, dessa uppgifter finns inte som genomgång utan här är tanken att du skall kunna träna själv men samtidigt erbjudas en längre förklaring för att kunna förstå xyz delen på högskoleprovet. Du hittar en videogenomgång på en annan xyz del på kurssidan för högskoleprovet.
jonas
Undrar angående uppgift 12. Skall man bortse ifrån att arean aldrig kan vara 72cm2 i en sådan triangel med sidorna 12, höjden kan väl inte bli samma som sidorna?? Lite förvirrande.
jonas
Sorry läste fel, trodde dom var liksidiga….
Simon Rybrand (Moderator)
Ingen fara! 🙂
Mikael
Hej!
Fråga 10. Hur kommer det sig att P => 3⋅4+4⋅4=25 och inte 3⋅3+4⋅4=25
Är det bara en felslagning av tangent från din sida eller är det något jag missat? Matte är inte min starka sida.
Simon Rybrand (Moderator)
Hej Mikaela, det är en felslagning av tangent från vår sida. Ber om ursäkt för detta fel, det är korrigerat, tack för att du påpekade det.
Daniel
Fråga 10: Jag förstår Q och S, men på P och R får jag 25 respektive minus 25.
Simon Rybrand (Moderator)
Hej Daniel, tack för att du påpekade den felberäkningen. Svaret är förstås fortfarande Q och S men bra att alla delar är helt korrekta. Det är ordnat.
Matilda
Hej!
Angående svaret på fråga 12. Det är väl B) 32cm2? vilket går att läsa i officiella facit för provet. Lösningen är väl helt enkelt 8×8=64/2=32.
Det är därför fel svar i detta prov. (och kan bli lite förvirrande hur man egentligen ska lösa uppgiften).
Simon Rybrand (Moderator)
Hej Matilda, ja du har förstås helt rätt och vi har korrigerat både svar och förklaringen till uppgiften. Tack för att du påpekade detta.
Endast Premium-användare kan kommentera.