
Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Högskoleprovet matematik
/ Övningsprov och förslag lösningar
XYZ – del 2

Här kan du testa dig själv på ett gammalt högskoleprov på delen XYZ. Provet är från den kvantitativa delen hösten 2011.
Till den här lektionen finns det endast övningsuppgifter och ingen video. Du startar övningarna genom knappen ”starta”.
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (12)
-
1. Premium
Hur många liter motsvarar $ 2 m^3 $ och $ 87 cm^3 $?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
2. Premium
Vilket svarsförslag är lika med
$ \frac{ \frac{5}{12} }{ \frac{12}{7} } $Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
3. Premium
Vilket svarsförslag är lika med $ \frac{9}{0,01 – 0,001 } $?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
4. Premium
Vad är $ (–2)^3 + (–3)^2 $?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
5. Premium
Vilket svarsförslag motsvarar $ \frac{x}{x+2} + \frac{3x}{x+2} $
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
6. Premium
Vad är $ 4^{-\frac{1}{2} } $?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
7. Premium
Vad gäller för x om $ 9 < \sqrt{x} < 16 $?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
8. Premium
Medelvärdet av fyra tal är 6. Två av dessa tal är 2. Vad är medelvärdet av de två andra talen?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
9. Premium
I en blomvas finns det n blommor. Av blommorna är p procent röda. Vilket av följande uttryck representerar antalet blommor som inte är röda?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
10. Premium
ABC är en liksidig triangel. Bestäm summan av vinklarna s, t, u och v.
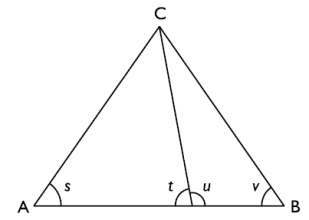 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
11. Premium
I svarsförslagen nedan är axlarna ritade i samma skala.
Vilket svarsförslag motsvarar linjen y = 3x – 3?
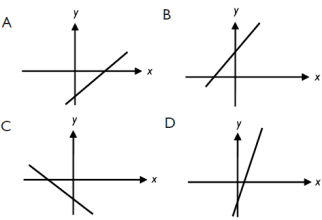 Bedömningsanvisningar/Manuell rättning
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar... -
12. Premium
Vad är xyz om $ x^2yz^3 = w^3 $ och $ xy^2 = w^9 $ ?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Liknande uppgifter: Högskoleprovet Högskoleprovet matematikRättar...

John Winlund
Uppgift 12, är inte upphöjt till en tredjedel samma som att dela med 3? Om man stryker potenserna i v.l och w^12 blir w^4?
Simon Rybrand (Moderator)
Hej, nej det är inte samma sak, däremot gäller att
$ a^{1/3}=\sqrt[3]{a} $
Yosef123
Tackar, hur kan man lösa fråga 6 4 upphöjt till − 1/2 . ska man tänka 1/4upphöjt 0,5? som är hälften av 2 eller tänker jag fel?
Simon Rybrand (Moderator)
Där behöver du känna till potensregeln $ a^{-b}= \frac{1}{a^b} $ samt att $\sqrt{a}=a^{1/2}$. Då får du att
$ 4^{-1/2}=\frac{1}{4^{1/2}}=\frac{1}{\sqrt{4}}=\frac12 $
Yosef123
Hej hur kan man göra
((xyz)3)13=(w12)13⇔
xyz=w4
på provet då man inte har miniräknare? hur ska man tänka och göra när man upphöjer något med 1/3 ?
Simon Rybrand (Moderator)
Hej
Det skall alltid gå att lösa utan räknare på provet och i det här fallet så använder vi potensregeln $(a^b)^c=a^{bc}$ för att kunna upphöja enkelt med 1/3.
Exempelvis
$ (2^3)^{1/3} = 2^{3⋅\frac13} = 2^{\frac33} = 2^1 = 2 $
David Stephan
Hej,
På fråga 11 är det lätt att missa -3 eftersom den hamnat under bilden och finns inte med i ekvationen.
Simon Rybrand (Moderator)
Har fixat med formateringen där så jag hoppas att det är enklare att se nu, tack för att du sade till!
kristinklinth
Hej!
Jag har en fråga om uppgift 12, i lösningen ställer du upp sambandet:
(x^2yz^3)⋅(xy^2)=w^3⋅w^9⇔
x^3y^3z^3=w^12⇔
(xyz)^3=w^12
Jag förstår inte riktigt hur (X^2YZ^3)*(XY^2) blir x^3y^3z^3, har du möjlighet att förklara det?:)
Simon Rybrand (Moderator)
Hej
Där använder vi potensregeln $ a^b⋅a^c = a^{b+c} $ för potenserna med baserna $x, \, y, \, z$.
Då får vi
$(x^2yz^3)⋅(xy^2) = x^2⋅x⋅y⋅y^2⋅z^3 $
$= x^{2+1}⋅y^{1+2}⋅z^3 = x^3⋅y^3⋅z^3$
TM
Hej på fråga 7 svarade jag 3 < x < 4 och fick fel, jag förstår inte riktigt var felet ligger? Tack för en bra sida 🙂
Simon Rybrand (Moderator)
Hej,
Förstod du förklaringen där vi upphöjer alla delar i olikheten med 2? Anledningen till att detta görs är för att vi enklare skall se villkoren för x vilket är svårare då vi har roten ur tecknet kvar.
Julia
Hej och tack för en jättebra sida!
Jag undrar i uppgift 12, finns det någon typ av formel för hur man kan multiplicera ihop de två ekvationerna eller är det något man i princip alltid kan göra?
Sedan undrar jag också ifall det är samma svårighetsgrad på uppgifterna på denna sajten som på högskoleprovet? Ifall man behärskar uppgifterna på denna nivån, borde man även klara uppgifterna på hp?
Tack på förhand!!
Simon Rybrand (Moderator)
Hej, Börjar med fråga 2:
De uppgifter du hittar här är tagna från gamla högskoleprov så det är ungefär samma nivå. Det finns ännu fler att träna själv på hos studera.nu. Jag rekommenderar dig att träna mycket på dessa också.
Fråga 1: Den uppgiften är lite av ett klurigare slag och tyvärr finns ingen stegmetod eller formel som alltid går att använda. Däremot används förstås mycket av grundförståelsen för ekvationer, potenser och bråkräkning.
Ellen
Hej!
Förstå inte riktigt fråga nr 4.. (-2)3 + (-3)2.
Svaret ska bli -8+9=1 har ni skrivit.
Man räknar väl (-2) * (-2) * (-2), men jag får det att bli 4. Och (-3) * (-3) blir 9. Förstår inte riktigt…
Tack för svar!
annelie.b
Hej,
Har två frågor:
Fråga 8:
Hur blir 4+A+B/4 = 6*4 (antar att det är så du tänker när du har 24 i nästa led)? Varför förkortar inte 4:orna bort varandra på vänster sida om = tecknet så att sexan står själv kvar?
4+A+B/4 =6⇔
4+A+B=24⇔
Fråga 12: Hur vet man att man ska upphöja med 1/3 i sista ledet av uträkningen? när man alltså är vid xyz^3 = w^12
Tack på förhand,
Annelie
Simon Rybrand (Moderator)
Hej
Fråga 8:
Där förlänger vi med 4 både i VL och HL, dvs
$ \frac{4 + A + B}{4} = 6 $ (*4)
$ \frac{4*(4 + A + B)}{4} = 4*6 $
Här tar 4:orna ”ut varandra” i VL vilket ger
$ 4 + A + B = 24 $
Fråga 12
Det beror på att vi har $ (xyz)^3 $ och det är $xyz$ som söks i uppgiften. Ett sätt att bli av med upphöjt till 3 är därför att upphöja med $\frac{1}{3}$. Värt att noter att detta är samma sak som att ta tredjeroten ($\sqrt[3]{ }$)ur bägge leden, hoppas att detta hjälper dig vidare.
annelie.b
Hej, Tack ! Jag förstår dina förklaringar till båda talen. Har en följdfråga bara – matteboken visar i hur man räknar tredjeroten ur med miniräknare, men på högskoleprovet är det huvudräkning som gäller. Hur tänker man för att (snabbt) kunna räkna tredjeroten ur i huvudet?
Eller är det lättare att tänka ”upphöjt till 1/3”, och är det i så fall bäst att dela talet (12 i exemplet) i tre delar (varje del blir 4) och då vet man att 1/3 är 4?
Har du några andra tips/sätt att tänka?!
Tack på förhand,
Annelie
Simon Rybrand (Moderator)
Hej,
Det är svårt att beräkna tredjeroten ur med huvudräkning om det är tal där man inte enkelt inser tredjeroten.
Exempel på enklare tal kan vara
$ \sqrt[3]{27} =3 $
$ \sqrt[3]{8} = 2 $
$ \sqrt[3]{64} = 7 $
Så jag tror att de på högskoleproven ofta väljer tal där man med hjälp av antingen lite olika test eller träning kan ta just tredjeroten ur.
I uppgiften här ovan så är det förstås lite annorlunda då vi har ^3, då blir man helt enkelt av med ^3 genom att göra motsatsen till detta, nämligen att ta tredjeroten ur.
sanchez021
Hej! grymt bra sida, Tänkte bara att om man har fel på en uppgift (t.ex 9) så skulle det vara bra om man hade någon snabblänk att klicka på så man direkt kom till vad man behövde plugga på mer!
Mvh!
Simon Rybrand (Moderator)
Hej, vilken bra idé. Det kan vi ganska enkelt ordna men kanske kan vara svårt att hinna innan årets högskoleprov, tack för ditt förslag!
Alwisw
Eller nu tror jag att jag förstår. 🙂
Simon Rybrand (Moderator)
🙂
Alwisw
Fast just det, glömde fråga – på den sista uppgiften, hur kan x^2yz^3 vid utbrytning bli ((xyz)3)^1/3? Det är här jag inte riktigt hänger med.
Alwisw
Hej!
På 3:an förstår jag inte lösningen med grundpotensform. Kan du förklara den lite närmare? Själv räknade jag att 9/0,001-0,001 = 9/(1/10^2-1/10^3) = (9/1)/(900/100 000)=900 000/900 =1000 men detta kanske är ett högst ineffektivt sätt på högskoleprovet under tidspress? Skulle verkligen vara bra om jag kunde förstå lösningen i förklaringen här på sidan.
Sen undrar jag över sista uppgiften, 12:an – Jag förstår inte hur det kan bli ((xyz)3)^1/3=(w12)^1/3⇔xyz=w4
Simon Rybrand (Moderator)
Hej,
Det finns såklart olika sätt som går olika snabbt för olika personer. Ofta märker jag att det sätt jag själv använder ibland tar längre tid för elever.
Men om jag skall förklara varför man kan gå över till grundpotens i den uppgiften så är det för att enkelt kunna tillämpa potensregeln:
$ \frac{a^m}{a^n} = a^{m-n} $
I uppgiften får vi då
$ \frac{9 \cdot 10^0}{9 \cdot 10^{-3} } = 1 \cdot 10^{0-(-3)} = 1 \cdot 10^3 = 1000 $
Även på den sista uppgiften så är det en potensregel som blir viktig nämligen:
$ (a^b)^c = a^{bc} $
Så om vi skriver den uträkningen tydligare så får vi:
$ ((xyz)^3)^{ \frac{1}{3} } = (w^{12})^{ \frac{1}{3} } \Leftrightarrow $
$ (xyz)^{\frac{3}{3}} = w^{\frac{12}{3} } \Leftrightarrow $
$ (xyz)^{1} = w^{4} \Leftrightarrow $
$ xyz = w^4 \Leftrightarrow $
Alwisw
Tack snälla du! Detta hjälpte oerhört. 🙂
Endast Premium-användare kan kommentera.