Lägg till som läxa
Lägg till som stjärnmärkt
Frågor hjälpmarkerade!
Alla markeringar försvinner.
KURSER /
Matematik 5
/ Derivata och Integraler – Ma 5
Träna mer på Förändringshastigheter och Derivata - Kedjeregeln
Formler och begrepp som används i video och övningar
I den här lektionen går vi inte igenom grunderna kring förändringshastigheter och derivata och tillämpningar på kedjeregeln utan tränar på fler exempel. Däremot kan följande begrepp och formler vara bra att känna till.
Sammansatta funktioner
Funktionen $ y = f(g(x)) $ är en sammansatt funktion där $f(g(x))$ är den yttre funktionen och $g(x)$ är den inre funktionen.
Sammansatta funktioners derivata – Kedjeregeln
Derivatan av en sammansatt funktion ges av kedjeregeln vilken säger att
$ y´= f´(g(x))⋅g´(x) $
där
$ f´(g(x)) $ kallas den yttre derivatan och $g´(x)$ den inre derivatan.
Exempel i videon
- Utanför ett hus står en cylindrisk tunna och samlar vatten. En dag regnar det i en jämn takt så att tunnan fylls på med 1,5 liter per minut. Hur snabbt stiger vattenytan i tunnan om tunnans radie är 60 cm?
- Zara är på en nöjespark och står och tittar på attraktionen ”The Rocket”. Hon står på plan mark 20 meter från attraktionen. Hon har fått reda på att när The rocket befinner sig på 21 meters höjd på väg uppåt så är dess hastighet 15 m/s. Hur snabbt ändras i denna tidpunkt Zaras avstånd c till ”The Rocket”?
Kommentarer
██████████████████████████
████████████████████████████████████████████████████
e-uppgifter (2)
-
1. Premium
Yvonne har fått följande uppgift.
”Ett rätblock har bredden $10\,cm$ och djupet $5\,cm$. Höjden minskar med $0,3\,mm$ per sekund och är vid en viss tidpunkt $12\,cm$.
Beräkna förändringshastigheten av volymen med avseende på tiden vid just denna tidpunkt.
Endast svar krävs”
Hon svarar på uppgiften på följande vis: $ \frac{dV}{dt}=\frac{dV}{dh}⋅(-0,03) $
Vad anser du om hennes svar.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
2. Premium
En cylinder har radien $r$r och höjden $h=3r$h=3r . Dess volym $V$V förändras med tiden $t$t. Vad kan ersätta $X$X i uttrycket nedan?
$\frac{dV}{dt}=X\cdot\frac{dr}{dt}$dVdt =X·drdtBedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...
c-uppgifter (5)
-
3. Premium
En cylinderformad silo används för att förvara säd. När silon töms görs det med hastigheten $ 3 \, m^3 $ säd per minut. Silons radie är $5$ meter. Hur förändras höjden på säden i silon under tiden den töms?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
4. Premium
En högtalare skickar ut ett högt ljud i alla riktningar så att det sprider sig cirkulärt så att dess radie vid en tidpunkt ökar med $337,5 \, m/s$. Vid denna tidpunkt är radien $1,20\, km$. Hur snabbt ökar arean av denna cirkel vid denna tidpunkt?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
5. Premium
En vätska silas genom ett filter som har formen av en rak cirkulär kon med spetsen nedåt. När vätskenivån i filtret är $8,0$8,0 $cm$cm sjunker den med hastigheten $1,2$1,2 $cm/min$. Vätskeytans radie är vid detta tillfälle $4,5$4,5 $cm$cm. Med vilken hastighet rinner då vätskan ut från filtret?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
6. Premium
Oscar står och tittar på när ett tåg åker förbi. Han befinner sig vid en tidpunkt $120$ meter från tågets slut och tåget är $180$ meter långt. Tåget har hastigheten $33 \, m/s$. Hur snabbt ökar avståndet mellan Oscar och tågets början vid denna tidpunkt?
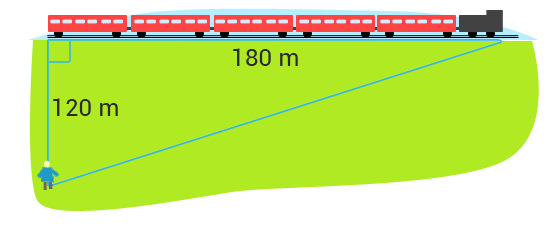Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar... -
7. Premium
En grön blomvas har en oval bottenyta och raka kanter. Dess höjd är $22$22 $cm$cm och bottenytans area är $48$48 $cm^2$cm2. En blå vas har formen av en rak cylinder med diametern $11$11 $cm$cm och höjden $19$19 cm. Båda vaserna fylls på med vatten. Vattenflödet är $4,0$4,0 $liter/min$. Jämför hur snabbt vattennivåerna stiger i respektive vas då de är halvfulla.
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...
a-uppgifter (1)
-
8. Premium
I ett koordinatsystem rör sig en punkt från origo, uppåt längs med $y$y-axeln med konstant hastighet. En annan punkt befinner sig på $x$x-axeln. Avståndet mellan punkterna är konstant. I ett visst ögonblick har punkterna koordinaterna $\left(6,0\right)$(6,0) och $\left(0,3\right)$(0,3). Med vilken fart rör sig punkten på $x$x-axeln mot origo i detta ögonblick?
Bedömningsanvisningar/Manuell rättningRätta själv Klicka i rutorna och bedöm ditt svar.-
-
Rättad
-
+1
-
Rättad
Rättar...
Kevin Lewis
uppgift 1 i förklaringen det ska väl vara,
visar: dV/dt och inte dV/dh
Anna Admin (Moderator)
Fixat.
Simon Rybrand (Moderator)
Hej
Tack för din kommentar, jag har förtydligat hur man kan definiera b på ett bättre sätt i uppgiften. Dvs detta kan inte sägas vara tågets längd utan avståndet från den punkt som Oscar tittar på vid tågets början till tågets start. Detta avstånd kommer att förändras med tågets hastighet.
maggix
Hej ser ut som ni snurrat ihop bokstäverna (a,b coh c) i svaret till uppgift 4.
Ni säger oxå att ”tåget åker med en hastighet på 33m/s” sen att ”Vi känner till att b förändras med 33 m/s och att a inte förändras alls så vi sätter din att dadt=0 och dbdt=33”
stämmer verkligen det? b borde väl inte ändras i samma hastighet som tåget hastighet? eller är det jag som tänker fel?
Endast Premium-användare kan kommentera.